CODE FESTIVAL 2016 予選A D - tookunn’s diary

問題

code-festival-2016-quala.contest.atcoder.jp

考察

まず問題文にある式がどういうものかを考えてみる。
(左上の整数) + (右下の整数) = (右上の整数) + (左下の整数)を $(i,j) + (i + 1,j + 1) = (i,j + 1) + (i + 1,j)$ と考える。
そしてこの式を変形すると,
$(i,j) - (i,j + 1) = (i + 1,j) - (i + 1,j + 1)$ または
$(i,j) - (i + 1,j) = (i,j + 1) - (i + 1,j + 1)$ となる。
この変形した式が表すのは,列 $j$ と列 $j + 1$ 間の値の差は行 $i$ と行 $i + 1$ で同じであるということで,これは行と列を逆にしても同じことが言える。

となると
$(i,j)-(i,j+1)=(i+1,j)-(i+1,j+1)=(i + 2,j)-(i + 2,j + 1)...$
という風にすべての行において $(i,j) = (i,j + 1)$ が成り立ち, 列 $j$ にある値と列 $j + 1$ にある値の差は必ず一意になることが分かる。
これも行と列を入れ替えても同じことが成り立つ。

また $(i,j)$ の値と $(i,j + 2)$ の値の差もすべての行において等しいことが分かり、
これは $(i,j) - (i,j + 1) = (i + 1,j) - (i + 1,j + 1) = (i + 2,j) - (i + 2,j + 1)...$ から列 $j$ と他のすべての列との差がすべての行において等しいということが分かる。

ある列 $k$ を基準にし,列 $k$ を0と考え,列 $k$ と他の列 $(0 \le i \lt C)$ との差を $x_i$ とする。
また行についても同じように考えることが出来て,ある行 $k$ と他の行 $(0 \le i \lt R)$ との差を $y_i$ とする。

以上のことを含めると $b_{i,j}$ は行 $i$ であり,列 $j$ に存在する値とし、
$b_{i,j} = x_j + y_i$ を求めることが出来る。

	$x_0$	$x_1$	$x_2$
$y_0$	$b_{0,0}$	$b_{0,1}$	$b_{0,2}$
$y_1$	$b_{1,0}$	$b_{1,1}$	$b_{1,2}$
$y_2$	$b_{2,0}$	$b_{2,1}$	$b_{2,2}$

そして,この $x_j(0 \le j \lt C)$ と $y_i(0 \le i \lt R)$ を頂点にして，与えられた $a_i(0 \le i \lt N)$ を頂点 $x_{r_i}$ と頂点 $y_{c_i}$ 間をつなぐ辺としてグラフにして考える。

適当な頂点から始めて辺を辿っていき, $x_j + y_i = a_k$ となることを目指し各頂点を通り, $x_j,y_i$ を求めていきます。
この辺を辿っていく操作は各連結成分ごとに行います。

最終的に $b_{i,j} = x_j + y_i$ となっているか矛盾しているかを判定することができます。
ここで,問題の制約上各マスの値は非負整数となっているので、必ず各マスの値が0以上の値になっていなければなりません。
もし、 $x_j + y_i \lt 0$ の組み合わせが存在する場合は0以上の値に収まっていないマスが存在するので、解は「No」になります。

例)問題ページのサンプル4

	$x_0$	$x_2$
$y_0$	$0$	$10$
$y_1$
$y_2$	$10$	$20$

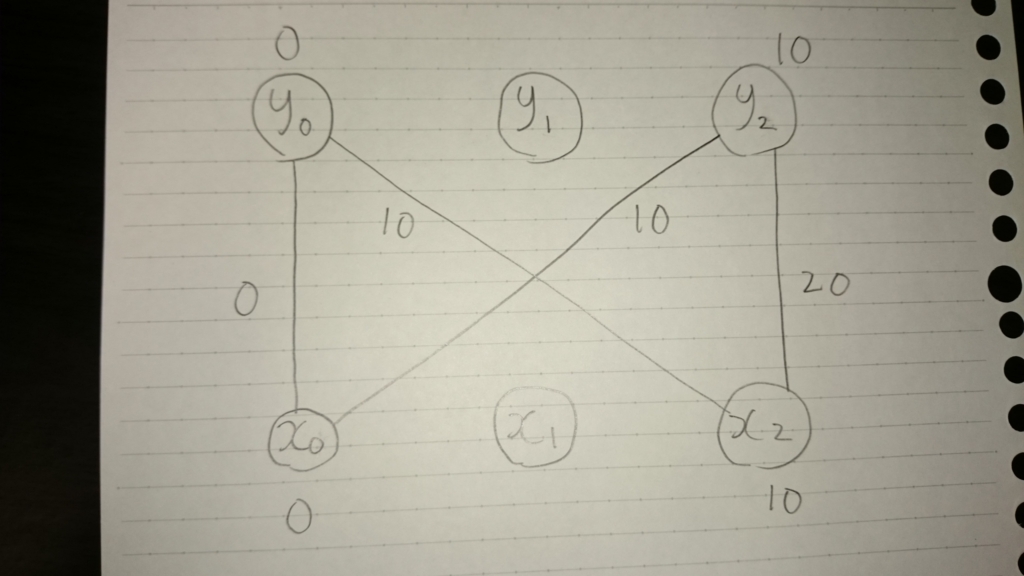
まず,上記で示したように入力で与えられたN個の辺を重み $a_i(0 \le i \lt N)$ にして,頂点 $x_{r_i}$ と頂点 $y_{c_i}$ に張る。
それから,適当な頂点を選びます。今回の例では $y_0$ を選んでいます。 $y_0$ から辿っていき,それぞれ $x_i(0 \le i \lt C)$ , $y_i(0 \le i \lt R)$ を求めていきます。
今回の最初に辿る先としては $x_0$ と $x_2$ があります。
式 $a_i = x_{c_j} + y_{r_i}$ から,辺の重みはつながっている二つの頂点の重みの合計と同値になっていなければならないので,頂点の一方でも重みが分かっていれば,
$y_{r_i} = a_i - x_{c_j}$ みたいに式を変形して求めることが出来ます。
以上から $x_0 = 0,x_2 = 10$ となります。
そして, $y_2 = 10$ となり,すべての辺について $a_i = x_{c_j} + y_{r_i}$ が成り立つので、Yesとなります。

例)問題ページのサンプル2

	$x_0$	$x_1$	$x_2$
$y_0$	$0$	$10$	$20$
$y_1$	$30$		$40$

f:id:tookunn:20160926213218j:plain
今回も適当な頂点として、 $y_0$ を選び, $y_0 = 0$ とします。
そして,最初に辿る頂点は $x_0,x_1,x_2$ になり, $x_0 = 0,x_1 = 10,x_2 = 20$ となります。
ここで、最後に辿る $y_1$ が問題になります。
$x_0$ から $y_1$ に辿ると $y_1 = 30$ になりますが,そうなってしまうと $y_1 + x_2 = 50$ になってしまい, $y_1,x_2$ 間の辺の重みと異なってしまうので,
今回はNoという結果になります。

公式解説
http://code-festival-2016-quala.contest.atcoder.jp/data/other/code-festival-2016-quala/editorial.pdf

ソースコード

import java.io.IOException;
import java.io.InputStream;
import java.io.PrintWriter;
import java.util.NoSuchElementException;
import java.util.*;
 
public class Main {
	int R,C,N;
	int[] r,c,a;
	long[][] b;
	boolean[][] used;
	ArrayList<Edge>[][] graph;
	
	private class Edge{
		int t,w;
		public Edge(int t,int w){
			this.t = t;
			this.w = w;
		}
	}
	
	private class P{
		int type,pos;
		long weight;
		public P(int type,int pos,long weight){
			this.type = type;
			this.pos = pos;
			this.weight = weight;
		}
	}
	
	public void solve() {
		R = nextInt();
		C = nextInt();
		N = nextInt();
		
		r = new int[N];
		c = new int[N];
		a = new int[N];
		
		used = new boolean[2][];
		used[0] = new boolean[R];
		used[1] = new boolean[C];
		
		b = new long[2][];
		b[0] = new long[R];
		b[1] = new long[C];
		
		graph = new ArrayList[2][];
		graph[0] = new ArrayList[R];
		graph[1] = new ArrayList[C];
		
		for(int i = 0;i < R;i++){
			graph[0][i] = new ArrayList<Edge>();
		}
		
		for(int i = 0;i < C;i++){
			graph[1][i] = new ArrayList<Edge>();
		}
		
		for(int i = 0;i < N;i++){
			r[i] = nextInt() - 1;
			c[i] = nextInt() - 1;
			a[i] = nextInt();
			
			graph[0][r[i]].add(new Edge(c[i],a[i]));
			graph[1][c[i]].add(new Edge(r[i],a[i]));
		}
		long[] min = new long[2];
		for(int i = 0;i < N;i++){
			if(used[0][r[i]])continue;
			Queue<P> q = new ArrayDeque<P>();
			//type,pos,weight
			min[0] = Long.MAX_VALUE;
		    min[1] = Long.MAX_VALUE;
			q.add(new P(0,r[i],0));
			while(q.size() > 0){
				P p = q.poll();
				if(used[p.type][p.pos])continue;
				used[p.type][p.pos] = true;
				min[p.type&1] = Math.min(min[p.type&1],p.weight);
				b[p.type][p.pos] = p.weight;
				for(Edge e : graph[p.type][p.pos]){
					q.add(new P(((p.type + 1)&1),e.t,e.w - p.weight));
				}
			}
			
			if(min[0] + min[1] < 0){
				out.println("No");
				return;
			}
		}
		for(int i = 0;i < N;i++){
			if(a[i] == b[0][r[i]] + b[1][c[i]])continue;
			out.println("No");
			return;
		}
		
		out.println("Yes");
	}
 
	public static void main(String[] args) {
		out.flush();
		new Main().solve();
		out.close();
	}
 
	/* Input */
	private static final InputStream in = System.in;
	private static final PrintWriter out = new PrintWriter(System.out);
	private final byte[] buffer = new byte[2048];
	private int p = 0;
	private int buflen = 0;
 
	private boolean hasNextByte() {
		if (p < buflen)
			return true;
		p = 0;
		try {
			buflen = in.read(buffer);
		} catch (IOException e) {
			e.printStackTrace();
		}
		if (buflen <= 0)
			return false;
		return true;
	}
 
	public boolean hasNext() {
		while (hasNextByte() && !isPrint(buffer[p])) {
			p++;
		}
		return hasNextByte();
	}
 
	private boolean isPrint(int ch) {
		if (ch >= '!' && ch <= '~')
			return true;
		return false;
	}
 
	private int nextByte() {
		if (!hasNextByte())
			return -1;
		return buffer[p++];
	}
 
	public String next() {
		if (!hasNext())
			throw new NoSuchElementException();
		StringBuilder sb = new StringBuilder();
		int b = -1;
		while (isPrint((b = nextByte()))) {
			sb.appendCodePoint(b);
		}
		return sb.toString();
	}
 
	public int nextInt() {
		return Integer.parseInt(next());
	}
 
	public long nextLong() {
		return Long.parseLong(next());
	}
 
	public double nextDouble() {
		return Double.parseDouble(next());
	}
}

考察とか結構自分の頭の中を整理するために書いたようなものなので,他の人は分かりづらいものになったかもしれませんが,
少しでも何かの気付きの手助けになればと思い,記事にして残しておきます。
間違い,指摘等あれば遠慮なくどうぞ